Introduction

A paper co-authored with Matt Roughan, Simon Tuke (both from Adelaide University department of Mathematics and Statistics), Matt Wand from the University of Technology Sydney, and Randy Bush from IIJ explored a question on the pervasive use of HTTPS to secure web transactions: Is anyone being left behind? This paper which is in Arxiv is still in peer review. We think it exposes an issue which is worth exploring more widely: What level of rigour do we need for public policy decisions related to the Internet?

We argue that it should be a process comparable to that used in public health, economics and other planning, which puts higher demands on data analysis and statistics, that flow into the policy making processes.

At the IEPG session before the IETF 99 Meeting held in Prague, I gave a brief talk about some work the five of us have been engaged in since December of last year. We’ve been exploring three things:

1. Do we see people that cannot make secure web connection?
2. What are interesting statistical techniques to apply to data analysis? Can we do better than the usual standards applied to research in this community?
3. How should public policy questions be approached? What are the requirements for data, used to answer these kinds of questions?

HTTPS Everywhere?

The fundamental question of interest came up from a conversation with Richard Barnes. Richard was interested in the "HTTPS Everywhere" issue:

• A routine assumption is that content available online should be on HTTPS. Websites therefore use HTTP 302 redirects to "uplift" people into an end-to-end secured connection. There are lots of reasons to want to do this. And by now, we suspect that almost all of us are doing this routinely and don't even think about it any more.
• We’re no longer conscious of the "green lock" on the browser. The next thing - actively deprecating insecure connections - may be coming as a surprise.
• If we’re going to say “let's go down this path”, maybe we want to know who can’t go there.

Is there anyone out there, who can’t be taken up to a secure HTTP connection?

Richard asked if the APNIC measurement system could look at this. After some thought, we ran an experiment. And we think we found something: people who just can’t be taken up to HTTPS. But the question is: "What does this mean?"

That's when we started to perform more complex analysis. You can find more details about this entire process at the end of this article in Appendix A.

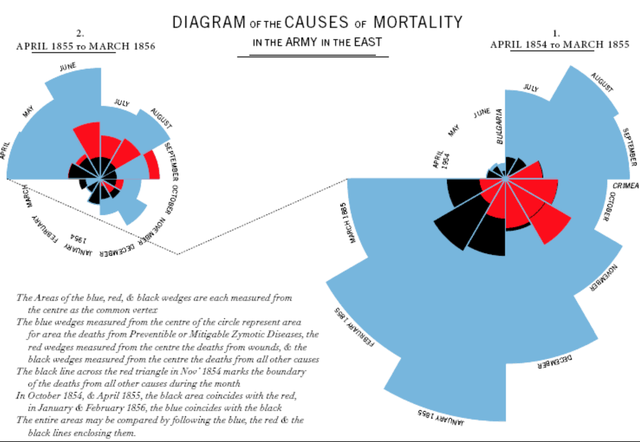
Original statistical analysis visulisation invented by Florence Nightingale

The statistician

In the experiment we saw an underlying signal: HTTPS is not exactly the same as HTTP and some people can’t do HTTPS in preference to HTTP.

Ok, job done. We could at this point in clean conscience say: ”Yes Richard, we can see a difference, some people have an issue with HTTPS” and move on.

But Matt Roughan and Randy wanted to push harder and understand the qualities underneath this.

So, the problem becomes not IF, but HOW MUCH. How can we tell how much something like region or economy or browser or operating system is causing this? And, given we had indications that it’s a weak signal, how do we distinguish it from the noise we know we had? At this point the skills of all three of the statisticians (Matt Roughan, Matt Wand and Simon Tuke) came in. Being able to talk to people in the data analysis community and find skills and brains to help on a problem is really valuable to anyone in my situation.

Statisticians are nice. They don’t actually care if the question is about kittens or atom bombs: they’re much more interested in the shape of the question and the problems inherent in the data:

• Is there a signal? How do you know?
• Is there noise? How do you know?
• How can you get away from being in love with your data?

Matt Roughan introduced me to a number of data models that helped to analyze the experimental data without being unconsciously drawn to patterns I expected to see. You can find much about these models in Appendix B.

Blinded data

At this point I was brought to realise that we (the network community) don't often "blind" the data we work. Sure, there are conversations about how to mask IP addresses, and that’s good for individual privacy and I think that’s very important, but blinding data isn’t about protecting the name of the mouse, its about preserving the objectivity around what is being said about mice in general.

Talking about treatment A vs. treatment B is different than talking about amputation vs. medication. Blinding is a way to maintain objectivity around the subject matter, and to stick to fundamentals:

• Can we show some effect with a degree of statistical validity?
• Can we be objective in what we’re seeing?

And carrying on from this, blinding leads naturally to reproducibility:

• If I give you my data, can you do the same things I did, and do you get the same results?
• Or, can you apply a different technique and get the same results? If not, why not? Does it mean we’re seeing different things, or different sides of the same thing, or the same sides of the same thing?

This isn’t new, but it is perhaps new for our domain of interest. We’re used to treating things in network operations and measurements a bit more loosely. We haven’t been acting like this is a question of public policy. In other domains people do this all the time: maintain objectivity, strive for reproducibility.

Matt Roughan suggested (and I concur) that we make the blinded data available. And it is: from the Arxiv site you can get our 3.3m sample dataset as a list of paired experiments with categories, and you can apply the same tests, the same models or different models. You can construct better models or find better tools for the same conclusions, or maybe disprove what we found.

This has moved beyond IP addresses, it's just statistics now. But statistics we can stand on, to inform the policy questions.

Florence Nightingale: inventer of the pie chart and my great-great-great aunt

The results

To come back to the initial question about how many people we leave behind when demanding the use of HTTPS, the outcomes were reasonably simple:

  1. Yes, we can confirm that a small number of people can’t be taken to a secure network connection if they start in an un-secure one. That means it has to be understood that the goal to have HTTPS everywhere is actually not achievable for everyone.

Is it a huge number? No. It's pretty small. But we can measure it, against noise in an experiment, so that means it’s a real thing. And we’re talking about real people in the real world: this isn’t some theoretical issue, it has consequences for users. So if we decided HTTPS everywhere was a MUST, we’d be saying explicitly that some people couldn’t get to some content.

What if that was preventing them from accessing government services? Or their own information? Or getting help?

 2. So a second aspect to the initial question is that it's not just about some economy, or one browser. We had a range of signals from different economies, ASNs and browsers. We think there are at least two, and probably more root causes here, and so we’re going to have to work a bit harder to find out why some people can’t use HTTPS.

The way APNIC measures is constrained, so we can’t give a good answer to ‘how many’ because we didn’t have a good random sample of people to compare to the global Internet. We had the subset of people google chose to pass us over HTTP only, where 95% plus are on HTTPS. So, somebody else is going to have to say how many people worldwide are currently not using HTTPS on a regular basis, and then we can discuss how the % figures we see (which are small) might apply.

Public policy decisions

This question How do we want to go into public policy decisions? is a really good one.

I think, and I think my co authors think, that we’re now deep into public policy drivers which in other domains like public health or transport policy or economics would require a lot more rigour than we often see applied in network measurements.

I think we’ve been skating around the issue for a long time. If this was a conversation about the applicability of a cancer treatment, or cost/benefit issues in the road network, we’d expect to see really robust, reproducible statistics applied, and we’d complain if the decision makers didn’t expect that. So, we think that for a lot of questions being explored in the Internet, we need a similar approach if they relate to a decision of consequence for everyone.

We should be using rigour. Rigour demands that hypotheses be well formed. Rigour demands that people test results, reproduce significant results and test theories.

Conclusions: where to go from here

What I learned from this experience is twofold:

Firstly it is possible to be in a domain of interest, conduct experiments and perform basic statistics for yourself. But this demands rigour which from time to time, I think we can all fail to meet. This is a shame, and I think the opportunity to work with statisticians is a big benefit. They are motivated to consider problems in abstract, but also maintain proper distance from the subject and stick to demonstrable outcomes which can be justified from the data. They use methods which can be re-applied, tested, verified, and in a sense re-examined because you commit to sharing data.

Secondly, when questions of utility in a public network come up, it is worth considering if you have moved from the "merely interesting" to a question which may become a matter of "public policy" or "the wider public interest". If that happens, you move from a domain where casual examination is ok, to one where rigour is needed, to ensure we don't make decisions based on faulty premises. This is the norm in almost all other matters of public policy where science engages: we consider things properly, precisely because so much vests in the decisions we make.

If you think that the Internet matters (and I do) then it's a logical conclusion to believe we need to be more overt about how we get our information for these important decisions: If you want it in medicine, or mining, or environmental sciences, you want it in the network.

We explored a couple of techniques of analysis which were completely new to me, and I very quickly got out of my depth. But I worked with very smart people who are used to doing this kind of public policy stats work, and who think we (the networks people) could talk more to them, and explore this. The paper has some good words on methodology and tools, and I recommend people to read it.

Appendix A: About the experiment

We had a 25 day experiment at the end of December 2016: We asked those people who came to us (the APNIC website) over HTTP (port 80), to get a pixel over TLS on port 443. We can only do this to people in port 80/HTTP. We can’t downgrade the 443 users to ask them to get an unprotected HTTP pixel, because that’s not allowed (you get a browser warning about insecure content, but we also said in the terms and conditions we wouldn’t do this).

We didn’t do any funny tricks with the encryption algorithm, or use an invalid certificate. We just did the simple test for now (it's a good question how people respond to odd certificates or new crypto algorithms or if they will still do a downgrade to RC4/40, but we didn’t explore that right now).

Something to bear in mind here, is that we don’t control the relative amounts of presentation by browser, or country, or provider. That’s not in our control right now. And, we can’t control how the users come in either on 80 or 443. So, the port 80 users could be a self-selected cohort who have issues in TLS to begin with. We don’t think so, because the results suggest most of them can do TLS. But its not random and we have to understand that.

And since the volume as a function of the global Internet use isn’t random, we can’t tell you by % how many Internet users worldwide have a problem here. We do think that what we see here would scale to indicate that, if we knew the relative proportions worldwide, but we don’t know that from this experiment.

So here is how I approached this problem naively at the start. I took these experiments, and I had the IP address of the user, and their browser string, and I was able to use the standard techniques: APNIC has to add Region and Economy by address, and Origin-AS from BGP using Geoff Huston's AVL tree tool, and I had a python package which took browser string and derives browser family and operating system family and version, and I did a simple tabulation: this many by each category, sortable.

But this is a really awful, crude way to look at data. And it’s almost impossible not to hone in to things and think "AHA! Smoking gun!" I have a signal. So you try to “see” Egypt (for instance) because you believe you read something last week saying Egypt is filtering twitter. Or you look for the UK because of the filter which BT is running. Or Cuba, or your own economy. Or your own ASN. Or Microsoft because you hate Internet Explorer.

This is just a fact of life: I look for patterns and inferences. And once I’ve made an ad-hoc inference, it's really hard to shed the burden. I keep coming back to confirm my suspicions.

From talking to people in the research community (e.g at AINTEC, and the IETF), I got taken pretty quickly to a sense that this is a problem in categorical statistics. We’re asking a simple yes/no question: can some people just not do this particular thing? Categorical questions go to the Chi squared test, and some downstream methods of asking if your hypothesis is rejected under some confidence limit. But I spent a lot of 2014 and 2015 skirting around the edge of something I am ashamed to admit: it is called ‘p jacking’ where you play with data techniques until you get a p value, a confidence value which gives you an "AHA" signal so you can stop p jacking and say at p=0.1 you believe you have a smoking gun. This is really bad. Its really unscientific. I had to step back from the brink on this, fall out of love with my data, and get some objectivity.

Emile Aben from the RIPE NCC was the one who recognised what I was doing, and brought me back from the brink: It's because he warned me about this kind of problem in science, I decided to reach out and get help. So I owe a huge debt of gratitude to Emile, for bringing me back from the brink.

Matt Roughan, the lead statistician I started to work with, gave me three strong requirements:

1. Firstly, he wanted the data blinded. He wanted all risk of subjective "AHA" moments removed. That was easy: I converted all the ASNs, economies, browsers and operating systems into different randomly selected unique codes, and I kept a map to reverse later on if need be.
2. Secondly, he made me sit down and try to formulate proper testable null hypotheses: things which could be subject to a statistical test at a confidence limit, and reduce it to a "meets or fails the test outcome", without any p-jacking.
3. Lastly, he suggested we’d be diving deeper into the toolchest, to find methods which went further.

So the long and the short of it is that the original question from Richard Barnes morphs into two distinct, but contextually related questions:

1. Given we had a control and an experiment, can we show there is no linkage between control and experiment? "Are they independent, even if both run by the same subject?"
2. And question two asks if, given we believe they have some degree of hardness, are they equally hard? They could be linked, but not equally hard.

Appendix B: Statistical models

Well, it turns out we have to reject both null hypotheses: we can show from the simple statistics that yes, they are linked. They are not fully independent, which is not surprising given they were run by the same subject: it’s a matched pair, and they tend to be heading to the same place overall: if you can’t do one, it's likely you can’t do the other. This comes from the application of fisher's exact test of independence of matched pairs: the data we had shows overall that we can’t accept that these are fully independent test and controls. They co-relate.

But, there is this second quality, which is ‘hardness’. And a different simple stats test - McNemars test - can exploit the fact that one of the pairs is a control: We asked the client to do four things, and required two of them to complete. Those two being fundamentally identical in all qualities to this control question. So given we know the two HAD to be done, and we have this control which is sometimes not being done, it's like a signal of ‘noise’ in the system. It's identifying the underlying randomness in the experiment. McNemar then says given a control and another test, is the test in any sense ‘harder’ than the control? And in our case, the result is yes: it is - formally we rejected a null hypothesis.

The answer is to use stronger statistical methods, and Matt was interested in exploring models. Finding a model which was a good analogy for the problem was, fitting the data to the model and then using the model to draw out distinctions in the categories. Can we use this to understand interelationships and co-factors?

Matt had an interest in a specific field, called item-response-theory. One of the older approaches in item-response theory, the Rasch model, says that there are latent - as in not understood - differences in the categories of some set of things, against some measure. Rasch models in this context take things and map them into a single line in ranking order. And applied to categorical questions, with a covariate of different values, they can rank by that covariate.

So for each of the qualities, region, economy, browser, OS, origin-AS we use a Rasch model, which is primed by the simpler statistics we had coming in to indicate (via the Fisher and McNemar tests) how the data was behaving, which then determined a ranking.

The second technique Matt Roughan wanted to explore is Generalized Linear Mixed Models, which is an established approach to data analysis, good at taking a number of qualities and finding out if they co-relate, so you can work out if they have stronger or weaker influence on the problem at hand. Matt Roughan reached out to colleagues in UTS and in his department which brought Simon Tuke and Matt Wand into the picture.

The paper goes into how the Rasch model is constructed and applied, but the quick answer is, it shows that there is a statistically significant difficulty in doing HTTPS compared to HTTP, which goes to differences by Browser or OS, by Origin-AS and economy. In both cases, to varying degrees, there are outliers which are more likely to show there is a problem.

So this is an indication that underneath the noise, we have a signal: there is some effect which can be ascribed to your ISP or economy, and that’s an effect about the network. But there is also an issue which goes to your browser or OS, which has nothing to do with the network you’re on, its about you and your platform. So immediately, we get this sense that there cannot be one underlying root cause, but we have a complex number of inputs that are hindering HTTPS. You might be exposed to one, or another, or all of them. It depends!

The thing is that the Rasch models showed that we had rankings, but we chose not to un-blind the data and find out which they are. We’ve decided to stay abstract and just treat these as distinct instances in some category, which we can show has diferential effect depending on value. We wanted to avoid objectifying the data.

The GLMM is a much more complex approach which I am happy to say I bascailly don’t understand. It appears to be a technique which is good at finding covariates, things which co-relate in their influence on the problem and therefore helps identify what's going on. Rasch models are really about a single category, and ranks within it. The GLMM ranks between categories.

Confirming our data collection methods

Applying these models had this useful adjunct of also confirming the APNIC method which has four distinct regions, did not overly influence the extent to which a problem can crop up by origin-AS or browser. So, given we measure in Singapore, the USA, Germany and Brazil I’m pretty sure we can say the actual economies of risk are widespread.

The strongest indication of a likely problem is the ASN, which in turn couples mostly to a specific economy, and economies relate directly to regions so its not surprising there is a marked association between these measures. However, we have distinct economy outliers, and ASN outliers.

Browser and OS also couple: there aren’t very many Internet Explorer browsers on Android (for instance) so again, there is a coupling.  But also there is a dimension here that the browser and OS don’t weight as much as the ASN do. So there is a strong and a weak influence on what's being seen. The problem divides up into network location and your platform - and they are independent.

So, in the broader sense, Matt Roughan and Randy made me much more aware that there is a huge issue out there in network measurement: We can do better.