The Internet is an object of study itself and scientists want to characterise different metrics, in particular QoS metrics (for example delays, bandwidth, or loss rates) with appropriate statistical models to improve their understanding of the performance of the Internet.

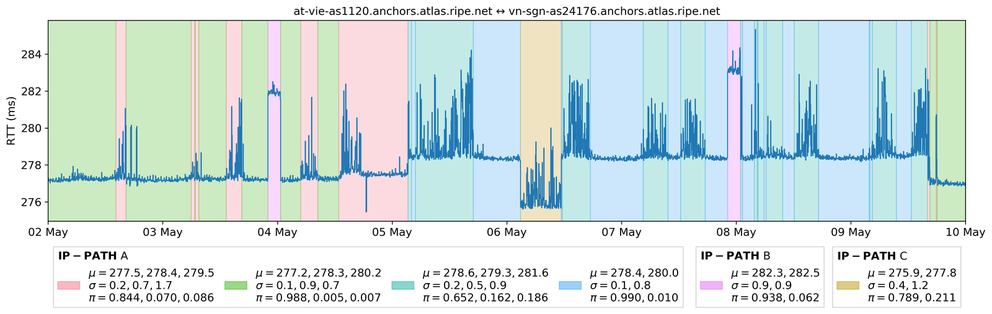
Because the impact BGP routing configurations and load balancing have on the end-to-end QoS, an analysis of time-series of delays on the Internet (such as RIPE Atlas RTT measurements) reveals a characteristic pattern of behaviour of these time series. It is normally the case that, for a given origin-destination pair, RTTs take on a small set of different values with some random fluctuations around these few base values. The different values may correspond to different routing configurations resulting in different Internet paths from source to destination, whereas the random fluctuations may be due to congestion or measurement errors. RTT values switch from one base level to another after a few hours, as can be seen in Figure 1.

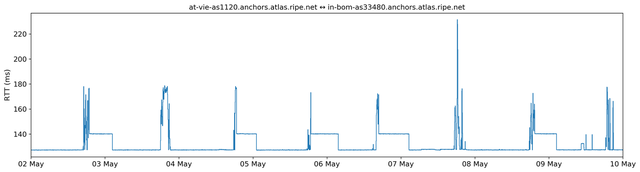
 Figure 1: RIPE Atlas RTT measurement between two RIPE Atlas anchors

From a statistical point of view this regularity can be explained by appropriate statistical models. We will show that Hidden Markov models (HMMs), and more precisely HDP-HMMs, are appropriate stochastic models for the characterisation of RTT series, explain how the parameters of these models can be trained and also discuss a bit what they can be used for.

HMMs and model estimation

A Markov chain is a stochastic process in a way that the Markov property is satisfied. That means, the current value of the process depends on the previous one only. HMMs are "noisy versions" of Markov chains: imagine a latent Markov chain, which is not observed directly, and observations that depend randomly on the latent Markov state. If we go back to our problem of RTT series, modeling the different “base levels” correspond to the states x(t) of the Markov chain. RTT values correspond to observations y(t), or a trajectory of a HMM (see Figure 2).

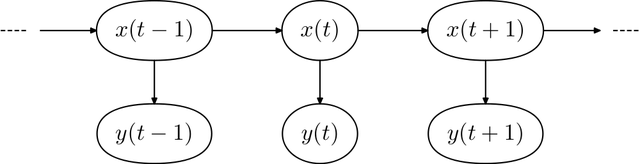
 Figure 2: Time evolution of an HMM, x(t) and y(t) are respectively the hidden state and noisy observation at time t

HMMs are parametric models. The stochastic model is specified by a few parameters only: the transition probabilities between states of the Markov chain, as well as the parameters of the probability distribution of observations given a particular state of the Markov chain (for example means and variances under a Gaussian distribution assumption).

So, a first problem is to calibrate the model parameters from the measurements. The Expectation Maximization (EM) is a standard training algorithm for HMMs. But in practice different problems are encountered when working with real data sets. A first common issue with EM is that it converges to a local maximum of the likelihood of the observations, and this maximum may not be the global one if the EM has not been initialised very carefully. A second problem is that the number of states of the Markov chain is often unknown (whereas it is supposed to be a known constant in EM).

For all these reasons we consider that a standard HMM model trained with EM is not a flexible enough approach to characterise RTT measurements. So far, several techniques have been proposed to cope with this problem. Recently efficient generic methods have been developed to estimate HMM parameters, that offer more flexibility to capture the variability observed in different kinds of real datasets.

The Hierarchical Dirichlet Process HMM (or, HDP-HMM [3], [4]) builds on Bayesian inference. The number of states of the HMM as well as the parameters of the probability distribution of observations in each state of the Markov chain are considered as random variables. In a Bayesian setting a prior distribution is assumed for the parameters. Then, the distribution of the parameters conditioned on the observations, a.k.a. the posterior likelihood, is the likelihood of the observations weighted by the prior distribution. Once this posterior distribution is obtained, it should be possible to obtain estimates of the parameters by looking at its mode or mean.

But in practice, the exact computation of the posterior distribution is intractable. However, samples from this posterior distribution, that is to say samples of the model parameters given a particular value of the set of observations, can be obtained using the MCMC (Markov Chain Monte Carlo) methods, in particular Gibbs sampling. MCMC methods are classical stochastic simulation methods for Bayesian inference [2].

For complex data sets, the problem of estimating the number of states of a HMM is not straightforward. A possible approach is to use Dirichlet Processes (DP) as priors for the number of states, which makes it possible to specify that the number of states is finite but unknown.

Moreover, in order to introduce enough flexibility in the model and to be able to accurately fit various real data sets HDP-HMMs are “hierarchical”. The model parameters (such as the transition probabilities of the Markov chain, and the means and variances of the Gaussian distributions of observations) depend on another layer of random variables and a “vague” prior is set on this root layer of randomness. This hierarchy of random dependences and vague priors introduces enough flexibility in the model to let it adapt to many different time series, such as audio recordings or… RTT measurements!

Experiments on RIPE Atlas measurements

We have explored this approach for the characterisation of RTT series using measurements from RIPE Atlas and an open-source implementation of HDP-HMM (see more on GitHub).

Built-in measurements between every RIPE Atlas anchors offer a comprehensive view of the QoS on the Internet: every 4 minutes pings and traceroutes are executed for each pair of anchors. Using the RIPE Atlas API we have assembled a dataset of 81,000 series, representing IPv4 RTT measurements between every pairs of anchors over one week. We considered the minimum value of the RTT at any given time slot, which resulted in 2,520 data points per series.

HMM parameters for each series have been learned using HDP-HMM. As a byproduct the Gibbs algorithm which has been used to fit parameters of the HDP-HMM model also infers the underlying states associated to measured RTTs. Some results are displayed in Figure 3. Here, a same background colour corresponds to the same value of the latent Markov chain. So, observations that belong to the same “cluster” are displayed on a background of the same colour. A visual inspection of many different clustering results has revealed that HDP-HMM is a very accurate model for RIPE Atlas RTT time series. In particular, it is possible to split the RTT time series into a small, yet homogeneous, set of clusters.

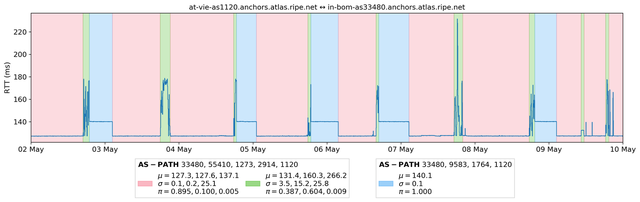
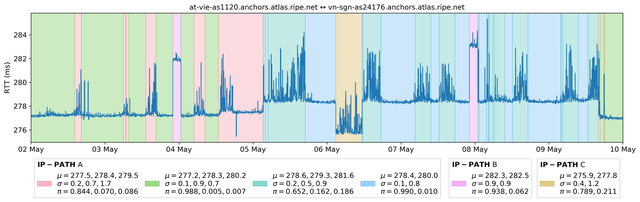
 Figure 3: States learned over a seven day period for RTTs measured between two RIPE Atlas anchors

One may wonder how many different states are necessary to characterise each origin-destination pair. So, we have processed a one week long dataset of RTTs between all pairs of RIPE Atlas anchors. And for each pair of anchors the number of states of the HDP-HMM model has been estimated.

Figure 4 shows a histogram of the number of states obtained. As one can see, for a vast majority of source-destination pairs five or six states are more than enough to capture the variability in the distribution of RTTs on a one-week long time period. 50% of the routes involves two or less states, and 99% six or less.

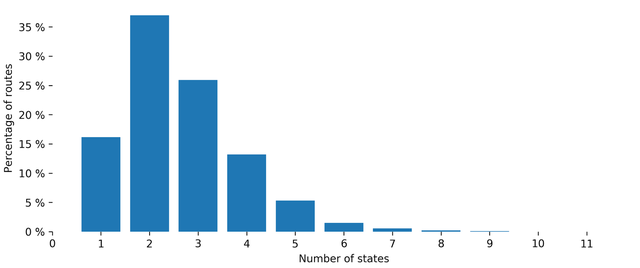
 Figure 4: Distribution of the number of states for models learned over one week

We then compared the number of states obtained on shorter timescales. Figure 5 displays the repartition of the number of states for periods of one day to one week. As one can expect, shorter periods lead to models with less states. 99% of the routes have four or less states for the two and three days long training periods, and three states or less for the one day period.

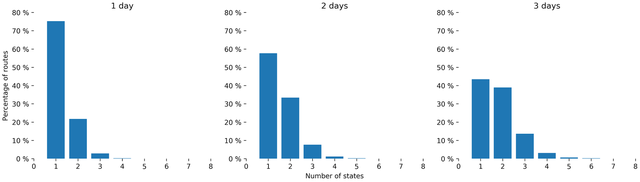
 Figure 5: Distribution of the number of states for different timeframes

Applications

You might wonder what this modelling is useful for apart from intellectual satisfaction.

Well, first of all, it can be used to derive performance metrics: mean and variance of the RTT in each state, average sojourn time in each state, probabilities of switching from one state to another, that can be more meaningful than global average performance metrics.

The proposed approach enables segmentation of the data with few persistent states and rapidly detect changes of state. This avoids the many false alarms that would arise with some other detection approaches.

The performance of different paths can also be compared statistically. For example, computing the probability that the delay is larger on one path or another between one source and one destination is quite straightforward once an accurate stochastic model has been calibrated.

In a next post we will investigate how such model may be used for network management.

If you want to learn more about the technical details, please refer to [5] and [6] (which will be published soon).

Bibliography

[1] Dempster, A., Laird, N., & Rubin, D. (1977). Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 39(1), 1-38.

[2] Robert, C.P., & Casella, G. (2004). Monte Carlo Statistical Methods (2nd edn.). SpringerVerlag, New York.

[3] Teh, Y. W., Jordan, M. I., Beal, M. J., & Blei, D. M. (2006). Hierarchical Dirichlet Processes. Journal of the American Statistical Association, 101(476), 1566–1581.

[4] Fox, E. B., Sudderth, E. B., Jordan, M. I., & Willsky, A. S. (2007). The sticky HDP-HMM: Bayesian nonparametric hidden Markov models with persistent states.