In this guest post, Max von Hippel provides an analysis of Karn’s Algorithm and the RTO computations described in RFC 6298.
The Internet consists of ‘protocols’ such as TCP, DCCP, SCTP, UDP, and so on. A protocol is a program allowing multiple computers to communicate information, such as emails or files. Since the Internet accounts for >3.4% of GDP in large and developed economies and undergirds essential infrastructure such as 911 services and power grids, we need to ensure that the Internet protocols work correctly.
At the NDS2 Lab at Northeastern University, we study Internet protocols using a variety of techniques for this very purpose. For example, in a prior blog post, I wrote about how we synthesised attacks against protocols given only their prose specifications. Today, I’ll zoom in on two critical components that are used in many Internet protocols — Karn’s Algorithm and the RTO calculation — and explain our recent efforts to formally verify them.
A common theme of Internet protocols is that they send data in chunks called ‘packets’. Sometimes packets are accidentally dropped in transit — like how an envelope could be lost in the mail. If a protocol wants to guarantee reliable delivery, it requires the receiver to acknowledge each received packet X with a corresponding acknowledgment, or ‘ACK’.
There are many varieties of ACKs, but the general principle is that the receiver informs the sender whenever it receives new data. In this work we study the most widely used type of acknowledgment, called cumulative ACKs, in which an ACK with value A acknowledges the receipt of packets 1, 2, …, A-1 but not A.
When a packet X is successfully transmitted from sender to receiver, and an acknowledgment A exceeding X is likewise successfully transmitted from receiver to sender, the sender knows that packet X was delivered (in fact, the sender knows even more; it knows that packets 1 through A-1 were delivered, but not A). If A is the first acknowledgement exceeding X to be delivered to the sender, then the time between when the sender sent X and received A is called the round-trip time (RTT) of X. The sender can sample the RTT to provide feedback on the pace at which it sends new data, so as not to overwhelm the network. On the other hand, if the sender never receives any ACK exceeding X, it can assume data was lost and retransmit accordingly. This scheme immediately produces two technical challenges.
Challenge 1: Suppose that the sender retransmits X, and then sometime later, for the first time, receives a corresponding acknowledgement A = X + 1. How does it know if the ACK is for the original transmission or the retransmission? In other words, how does it know if the original transmission was lost and the retransmission was delivered to the receiver, or if the original transmission was delayed, but ultimately delivered (and acknowledged) before the retransmission? Importantly, the sampled RTT will be either larger or smaller depending on the answer. This challenge is illustrated in Figure 1:
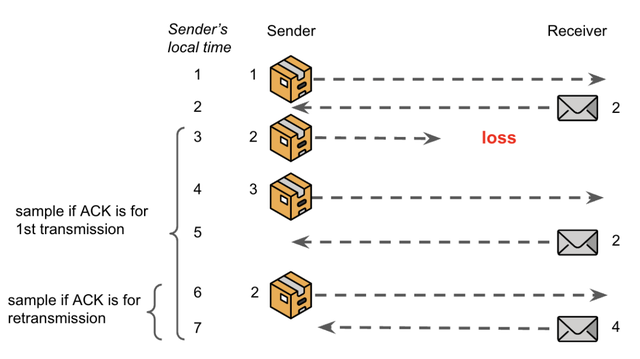
Challenge 2: What happens when the RTT goes to infinity? Put differently, how long should the sender wait for an ACK, before assuming the corresponding data was lost in transit, and retransmitting?
The most popular solutions to these two challenges are Karn’s Algorithm and the RTO calculation, respectively. In Karn’s Algorithm, RTT values are measured only for unambiguous ACKs, that is, ACKs for datum that were only sent once. If an ambiguous ACK arrives then the system assumes the RTT is unchanged since the last time it was measured.
The RTO calculation, meanwhile, is a recursive function over the measured RTTs and produces a Retransmission Time Out — an amount of time the sender should wait for a new ACK before assuming data was lost and retransmitting. Generally, protocols use these components in conjunction: RTTs are sampled with Karn’s Algorithm and then fed into the RTO calculation to compute a timeout. Our project was to define what it would mean for these systems to work correctly, and then, to determine whether or not they did. This is important because according to the Internet Engineering Task Force:
The Internet, to a considerable degree, relies on the correct implementation of the RTO algorithm […] in order to preserve network stability and avoid congestion collapse. -- RFC 6298
We took a formal methods approach, meaning we modelled the two systems mathematically, and then proved (or disproved) properties about each, inside of software systems that can automate some of the proof efforts and assure that there are no mistakes in the proof. We began by modelling Karn’s Algorithm in Ivy, an interactive verifier for inductive invariants. Ivy is especially well-suited to protocol modelling because it has built-in primitives for interleaved network semantics with communication and variable scoping, and because the properties it supports (inductive invariants) are well-suited to reasoning about protocol executions.
Our model of Karn’s Algorithm makes the following assumptions. First, the sender does not send X unless it has already sent 1 through X-1. However, the sender can retransmit any packet it has already sent. Second, ACKs are cumulative. Third, the network connecting the sender and receiver can lose, reorder, or duplicate packets or ACKs, but cannot create new ones. Note, most prior works required stronger assumptions, for example, ACKs are not reordered, or messages are never duplicated. Our theorems are stronger as they require fewer assumptions.
We prove the following. First, Karn’s Algorithm samples a real RTT, but a pessimistic one. If Karn’s Algorithm computes an RTT sample after receiving acknowledgments for X, Y, and Z, then that RTT will be the RTT of either X, Y, or Z, and will be ≥ the RTTs of the other two messages. Second, if the receiver-to-sender connection is FIFO in the sense that ACKs are not dropped, duplicated, or reordered, and if Karn’s Algorithm computes a sample upon receiving an acknowledgment A = X + 1, then X is equal to the highest ACK the sender received prior to A. This second scenario is the one most prior works considered since they ignored the possibility of a non-FIFO receiver-to-sender connection. These properties characterise the goals of the algorithm. Hence by proving Karn’s Algorithm satisfies these properties, we prove that it works correctly.
Next, we modelled the RTO computation using ACL2s, an interactive theorem-prover based on LISP. In contrast to Ivy, ACL2s does not have built-in semantics for interleaved network processes, but it does have support for rational numbers, which we needed to reason about the sequences of RTTs and corresponding RTOs.
The RTO calculation is based on two internal variables, recursively defined over the RTT samples, called the rttvar and srtt. Intuitively, the rttvar is meant to measure the degree to which the samples differ, which is at most the difference between the smallest and largest samples — and in fact, we prove that in the long run, the upper bound on the rttvar converges to exactly this difference. Meanwhile, the srtt is meant to give a ‘smoothed’ estimate of the RTT. It is therefore unsurprising that we prove bounds on the srtt, which over time, converge to exactly the bounds on the samples.
Unfortunately, we showed that these bounds do not imply an absence of timeouts (recall that timeouts should only really occur when there is congestion, because every timeout triggers retransmissions, slowing down the connection and potentially clogging up the network). A timeout can occur when the RTO is less than the RTT sample value Si. We show how even when the RTT samples are bounded, infinitely many timeouts could occur. Such a scenario is illustrated in the bottom half of Figures 2 and 3.
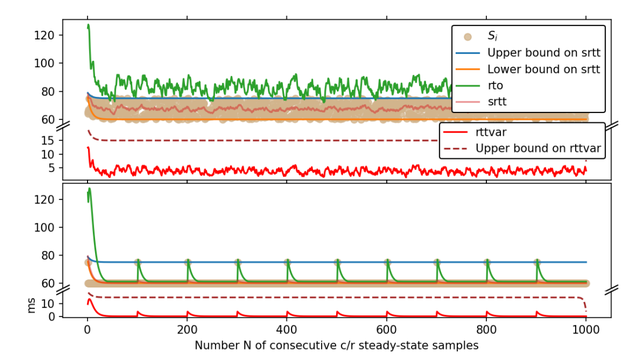
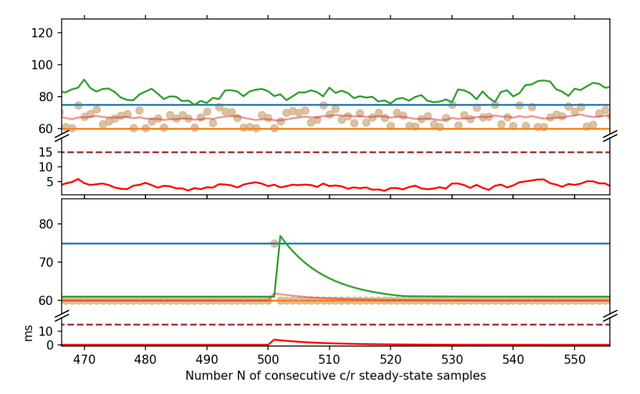
Further work is needed to precisely characterize the subset of steady-state conditions in which such edge cases cannot occur. Perhaps the requirements can be articulated by bounding the velocity and acceleration of the RTT sample values — but this is purely speculative.
This project was a collaboration with Lenore Zuck at the University of Illinois Chicago, as well as my advisor Cristina Nita-Rotaru at the Northeastern NDS2 lab, and Ken McMillan at the University of Texas at Austin. Lenore mentored me closely on this paper and it was an excellent learning experience. In addition, she recently presented the work at NETYS 2023 where we were honoured to win the Best Paper Award! Proceedings from that conference were published in Springer LNCS, including our paper. All our models and proof are open source and freely available on GitHub. We are very excited about this paper and hope future researchers build on our models to better understand the Internet, when it works correctly, and when it can fail!
This article was originally published over on the APNIC blog.


Comments 0