This analysis of RIPE Atlas traceroutes for days in 2012, 2015, 2017 and 2019 displays full network graphs for each successive half-hour and develops an algorithm for finding node or edge outages of an hour or more.
1. Introduction
RIPE Atlas is a large distributed measurement system, with about 10,000 small Linux-based probes at different locations around the world. The probes, available to researchers for ‘custom’ experiments, perform traceroute measurements using Paris traceroute to a set of ‘built-in’ destinations every half-hour. Traceroute data from these probes could be used to identify topology changes and/or BGP4 outages; this article considers how to achieve that.
In earlier work done in 2012 I developed a difference measure for successive traceroutes from a probe and used single-link clustering to find groups of probes with differences at (about) the same times. Although that work was promising, we were not able to use it to determine where in the Internet topology such differences had occurred.
In 2014, I spent some time at CAIDA, searching for a different approach. Brad Huffaker suggested it would make better use of all the RIPE Atlas data if we simply constructed a full topology graph from the traceroutes. Given such a graph, we could develop algorithms to find topology changes that cause outages for users in (one or many) Autonomous Systems (ASes), and perhaps use those algorithms in a system to give Internet Operators warning of such outages.
The ‘full-graph’ approach had the potential to produce huge Internet graphs; clearly we needed to understand the graph properties so as to produce datasets that could be handled effectively. Using sequences of such graphs, we could then develop techniques to find ‘significant’ changes in the Internet topology.
Questions to be answered:
- How could we choose a RIPE Atlas traceroute Destination that provides good coverage of the global Internet, or parts of it?
- How could we visualise our RIPE Atlas topology graphs?
- How could we find topology changes in our graphs that cause hundreds of traceroutes to fail, for periods of more than half an hour?
- How could we find a way to visualise those changes?
2. Datasets
2.1 Collecting Our RIPE Atlas Traceroute Data
The RIPE Atlas API provides two main components: Cousteau, a wrapper around the RIPE Atlas API, and Sagan, a parser for RIPE Atlas measurement results. Both components have Python modules that make them simple to use in Python programs.
For this paper, we collected a day of RIPE Atlas data for a chosen set of its built-in destinations; based on our earlier work we chose destinations with IDs 5017 (ronin.atlas), 5004 (f.root), 5005 (i.root), 5006 (m.root), 5015 (h.root) and 5016 (j.root), and days 22 Feb 2012, 20 Feb 2015, 20 Feb 2017 and 11 Dec 2019. At half-hourly intervals, each probe runs traceroutes; we divide each day into 48 ‘time-bins,’ one for each half-hour.
For each of our chosen days (above), we downloaded all the probe ID numbers for Cousteau’s ‘World-Wide’ area. From that list we randomly selected up to 10,000 probes. We downloaded RIPE Atlas data for traceroutes from our selected probes to a single destination over a single day, and saved it in gzipped files containing the data in json format.
2.2 Building the Graphs
Each of the probes makes a traceroute to each RIPE Atlas ‘built-in’ fixed destination once during every half-hour time-bin. So each of a dataset’s time-bins contains one set of traceroute data from all the probes active during that time-bin. We read the dataset’s gzipped file of RIPE Atlas json data and parse it (using Python’s json module) to get the traceroute results for all of its time-bins.
For each time-bin we build a graph from its traceroute data. We store each time-bin graph in a dictionary of nodes, with each node containing a dictionary of its edges. Each edge holds a ‘source’ node name and the number of incoming traceroute packets observed reaching the node from that source. The number of traceroute packets arriving at a node is thus the sum of the incoming packets from all its source nodes.
We create a nodes directory from the traceroute data; traceroute hops may add new (destination) node(s), and edges for the nodes in the preceding traceroute hop. Since traceroute data is inherently noisy, we clean up the data as we did in 2012 - i.e., by deleting RFC 1918 addresses (inside a probe’s host network), deleting empty hops and any edges that would create cycles in the graph. For responders that appear in several hops, we use the last hop in which they appeared.
To build a time-bin’s graph, we start at a root node - i.e., one that does not terminate edges back to any other nodes - and process its incoming edges. For destinations 5017, 5004, 5005 and 5006, we can start with the node for that destination. However, because destinations 5015 and 5016 had few successful traces, we needed to find another approach. Our algorithm for building the complete graph is therefore:
- Select as root_n the unmarked node with the most incoming traceroute packets
- Walk the graph from root_n, marking its nodes as subtree n
- Repeat for n = n+1 until all the nodes have been marked
When this algorithm finishes, it has produced a graph consisting of a set of separate trees for n roots. The graphs produced by this algorithm include all of the traceroute paths from all the probes.
Our Lenovo T61 computer (Intel Core Duo 2.2 GHz) takes about 1.6s per time-bin to produce the graphs. We saved the resulting sets of 48 trace graphs in graphs*.txt files.
We could then read the data from our (local) day/destination .gz files. The following table summarises our six datasets, identified by their RIPE Atlas msm_id (measurement ID) values. The statistics in this table are:
| statistic | Description |
|---|---|
| instances | Number of instances (for anycast root-servers) |
| n_traces | Number of traceroutes to this msm_id |
| tr success | Percent success for traceroutes |
| nodes | Number of nodes found per bin |
| asns | Number of ASNs found per bin |
| edges | Number of edges (between nodes) found per bin |
| edges_inter | Percent edges between different ASNs |
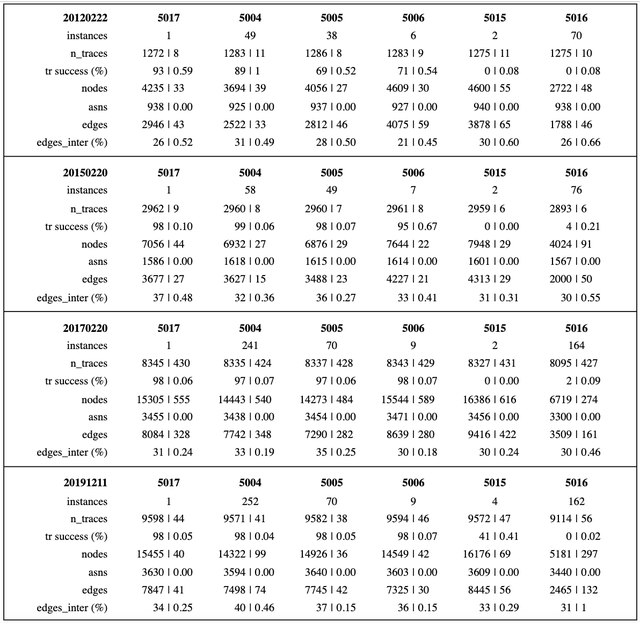
Table 1 summarises all our datasets for the six chosen destinations. Of these 5017 is a single host located in Amsterdam; the others are anycast root-servers, with various numbers of instances. Our statistics are for all nodes visited during traces for each day’s 48 time-bins, and are shown as mean | iqr - i.e., mean value for the day, and inter-quartile range for the day’s 48 time-bins.
On 20 December 2012, the probes all made about 1,275 traceroutes to their destinations. Traceroute success rates - i.e., percentage of traceroutes reaching their destinations - varied from 93% (5017) down to 69% (5005), however none of the traceroutes to 5015 and 5016 actually reached their target. Traceroutes to 5015 (h.root) were nearly all ‘administratively blocked’, which explains their zero success rate. However, 5016 (j.root) also had very low success rates, and traceroutes to it visited less than half as many nodes than for the other destinations. 5016’s behaviour seems surprising; perhaps future work to explain that could be interesting.
For the three later dataset dates (20 Feb 2015, 20 Feb 2017 and 11 Dec 2019), the values for most of our statistics increased. For example, the number of instances for each root-server had increased from 2017; in 2019, 5015 (h.root) had two new instances, and its success rate increased to 41%. Overall, our statistics values increased rapidly for 2015 and 2017, and then much more slowly for 2019. Interestingly, apart from the low success rates for 5015 (h.root) and 5016 (j.root), and the low number of nodes visited for 5016, there is little difference in a day’s statistics values for the other four destinations.
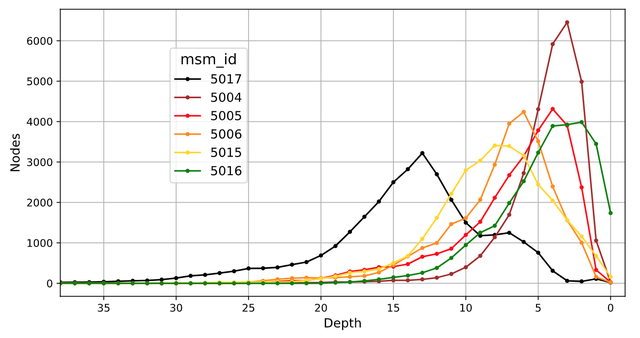
For our trace graphs we use the terms ‘proximal’ and ‘distal’ to mean ‘near to’ and ‘far from’ the destination, and ‘depth’ to mean ‘number of trace hops back from the destination.’ Nodes - i.e., the nodes in our traceroute graphs - are the hosts that responded to incoming traceroute packets. Thus, the destination node has depth 0, proximal nodes have depths 1, 2, ..., and the RIPE Atlas probes are the most distal nodes in our graphs.
Fig 1 shows the maximum number of nodes forwarding traceroute packets (source nodes) at depths 0 to 38 for all 48 traceroute graphs on 11 December 2019. Traces to destinations with high success rates produce graphs with a single ‘root’ node. Those destinations had only a few nodes at depth 0. However, 5015 had a few, and 5016 had many. Those two destinations had very low success rates, so their traceroutes ended in ‘sub-roots’ - i.e., nodes which did not forward traceroute packets to any other nodes. The traces to sub-roots, however, follow much the same paths in successive time-bins, so they are just as likely to see topology changes as those to root nodes.
The other anycast root-server destinations had high peak node counts at depths 3 to 8, with rapidly falling node counts for more distal nodes. Since those servers have many geographically distributed instances, their proximal nodes have short paths to each instance. 5017, on the other hand, has a single instance in Amsterdam, so its nodes at depths 1 to 3 lie within it’s service provider’s ASN; up to depth 13 its number of nodes increases, then falls slowly towards its distal nodes.
In section 2.2 above, we built network graphs for each time-bin, stored as a list of nodes, each with a dictionary of sources. Edges in our graphs are paths from sources to nodes. We observe that because the graph changes a little between time-bins, the set of nodes and edges in each time-bin’s graph are different. For example, for our 2019 data, Table 1 shows that there were 15455 | 40 nodes (mean | iqr) for msm_id 5017. To allow for those changes, we construct dictionaries of all-nodes and all_edges - i.e., the number of different nodes and edges seen over the whole day’s traceroutes.

Fig 2 shows cumulative plots of the all-nodes and all-edges counts for our six msm_ids. Its left-hand plot shows the size of all_nodes rising fairly rapidly up to about time-bin 13, then rising more slowly. Note that the number of nodes seen for 5016 (j-root) is much less than for our other destinations.
Fig 2’s right-hand plot shows the size of all_edges over the day; its shape is much the same as for all_nodes, but there are much fewer edges. The ratio of nodes/edges is about 1.3. That’s reasonable, since the outermost (most distal) nodes don’t have edges terminating on them; all the other nodes do.

In our graphs, a node’s in_count is the total number of trace_route packets sent to it from more distal nodes. Fig 3 shows cumulative distributions of in_count for all nodes found in the graphs for traces to each of our destinations (msm_ids). Since traceroute sends three packets to each more proximal node, these graph’s larger steps appear at multiples of 3 nodes. The upper plot shows the nodes with in_count 0 to 30; most of the outermost (most distal) nodes have in_counts of 3.
Fig 3’s lower plot shows the number of nodes with in_count 30 to 30,000 on a log scale. These rise steadily from in_count 30 to about 1000, and do not increase very much after that (up to 9572 nodes for 5016, and up to 23,134 for 5015). The dots on the plot show the in_count values that actually appeared in the trace data. For in_counts above about 280 the observed values become more sparse, showing that more proximal nodes receive more and more incomeing traceroute packets. Note that 5015’s (h.root) trace (yellow) stops at in_count 13,059, and 5016’s (j.root) trace stops at only 2190; that’s probably because of the low number of edges seen (edges in Table 1) by 5016.
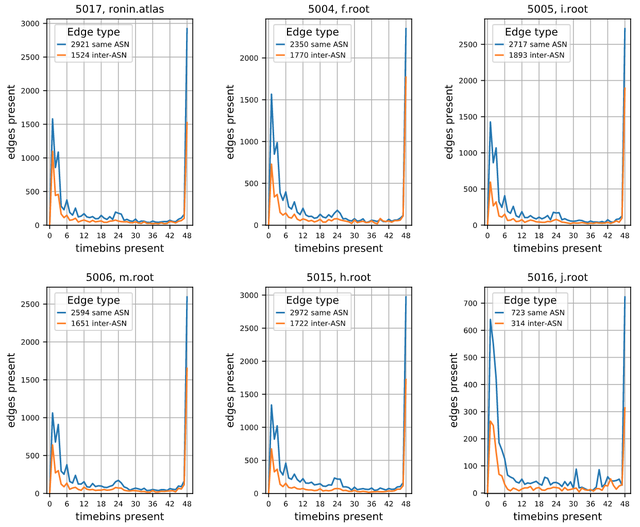
The plots in Fig 4 show the presence (in blue) for same-ASN edges - i.e., edge source and destination nodes in the same ASN - and (in orange) for inter-ASN edges - i.e., edges between two nodes in different ASNs. For each observed edge we count the number of half-hour time-bins it appeared in.
‘Stable’ edges are ones that were present in nearly all 48 of the day’s time-bins. Edges with lower presence were less stable. Note that a presence of 24 does not mean that the edge was present for 24 consecutive time-bins; edges can appear and disappear at any time!
The plots have very similar shapes. They start with small numbers of edges with presence 0 to 6. Then edge presence declines slowly for presence 7 to 22, and that’s followed by a small bump in presence 23 to 25 for same-ASN edges (but not for inter-ASN edges). There are few edges with presence from 26 to 46, then a large number of edges with presence 47 to 48 (the ‘stable’ edges).

Fig 5 shows the number of ‘stable’ edges - i.e., those present in all but two time-bins - for depths up to 38. The upper graph shows Same-ASN edge counts, and the lower graph shows Inter-ASN counts.
As depth increases, the Same-ASN edge counts rise to a maximum at depth 4, fall slowly to about depth 11, rise to a smaller peak at depth 13, then slowly fall to depth 29. Inter-ASN edges, however, have a maximum at depth 2, then fall from depth 5 to 9, rise again to depth 12, then fall slowly to depth 21. 5004, 5005 and 5006 have many instances, which probably accounts for their peak edge counts at depths 3 to 6 (proximal).
On inspecting our topology graphs, we see that proximal nodes tend to have many incoming edges, hence the rapid rise to depth 4. As we move to more distal nodes, the number of incoming edges decreases again - indeed, many of the traceroutes pass through many nodes before reaching any with more than one incoming edge. These low-incoming-edge nodes produce the slow rise through distal nodes to about depth 5.
Some of the RIPE Atlas nodes are ‘anchor’ nodes, each located at locations that have good Internet connectivity. Anchor nodes serve as traceroute targets, e.g., inside the country where they are located. They can also behave as trunk paths to our chosen destinations; that might give rise to the edge-count peaks in Fig 5 for depths 12 to 15.
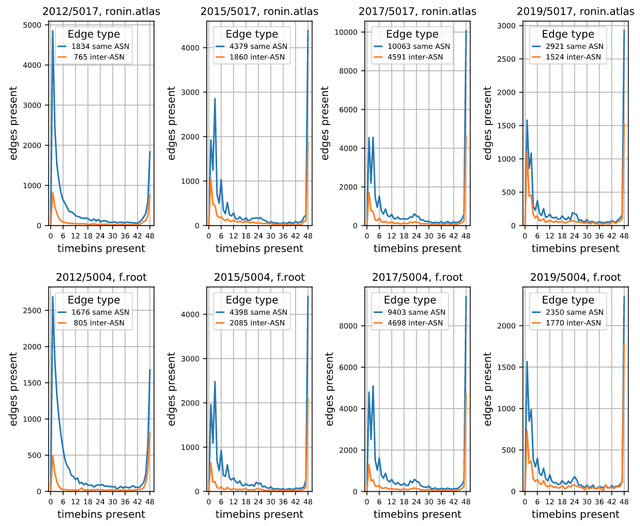
Fig 6 provides an overview of how Internet topology changed over the four years covered by our datasets. For this figure we chose Destination 5017 (single instance) and 5004 (highest percent inter-ASN edges) in our 2019 dataset.
Fig 6 is similar to Fig 4 (edges present v. presence), but it shows how the edge presence plots changed over our datasets' four years. For these two Destinations, the shapes of the presence distributions remained almost the same from 2017 to 2019. The 2012 datasets are different; the number of Inter-ASN edges is about the same as for the other years, but the number of Same-ASN edges is much higher. Again, the number of stable Inter-ASN edges in 2012 is much lower than that in later years.
Overall, Fig 6 seems to show that the fraction of edges present in 18 or fewer time-bins has decreased significantly from 2012 to 2019, suggesting that the Internet topology has become more stable for our datasets from 2012, 2015, 2017 and 2019.
3. Drawing and Viewing Graphs of the Datasets
3.1 Finding Autonomous System Numbers (ASNs) for Nodes
To find the ASN for our graphs nodes, we used CAIDA’s BGPStream to download the BGP data covering the graph’s dataset. Each address block was usually originated by a single ASN, but there were a few that were originated by several ASNs. For example, many European ASes appear to meet at a common exchange point; the BGP data shows that BGP routing information can leak through that exchange point; we use ‘3549|15576|6730|3356’ for its ASN. (Thanks to Emile Aben and Armogh Dhamdhere for this explanation!)
For each dataset, we use Python’s Radix module to make a radix tree, from which we look up the ASN for each observed node, thereby making a list of all the ASNs encountered by the dataset’s traceroutes. For each of the ASNs, we use whois to look up information about the ASN, in particular its owner’s name and country code. That information is stored as the node’s ‘tooltip’ data (section 3.4 below).
3.2 Making Graph-Image Sets
To make SVG images of each time-bin’s graph, we write a dot file of it’s graph, then use neato from graphviz to make an SVG image from it. To help see the changes between time-bins, each node must be drawn at the same position in each time-bin. To achieve that, we make complete lists of all the nodes and edges appearing in any time-bin and use dot to draw the resulting ‘whole’ graph, thereby producing a text file with each node’s x,y position. We then use those positions to draw all the time-bins’ graphs with neato.
graphviz is an effective tool for rendering graphs, but for our large graphs we were very much aware of the time it takes to produce each image. To minimise its processing time we set neato’s splines parameter to off.
The elapsed time needed to produce an SVG image has two components; the time to make it’s ‘whole’ graph using dot, and the time needed to render each time-bin’s graph as an SVG image. Both components depend on the number of nodes and edges in the graph. Referring to Fig 3 (a cumulative plot), we see that the number of nodes with in_count 30 or less is about 15,000, and that higher-in_count nodes add about another 6,000 nodes.
We investigated the effect of limiting graph size by ignoring nodes with in_count less than mn_trpkts. For mn_trpkts values 24, 18, 12 and 6, it took 0.60, 1.20, 2.67 and 58.14 seconds for dot to draw the whole graph. For the same set of mn_trpkts values the SVG rendering rate was 0.18, 0.23, 0.28 and 0.57 seconds per time-bin. For mn_trpkts = 3, we gave up after 3 minutes for the first time-bin!
Overall, we found mn_trpkts = 24 works well, producing large but still viewable SVG images while keeping production and browser rendering times acceptably low. Note that we only use a non-zero value of mn_trpkts when making SVG graph images for each of our datasets. For everything else (including Table 1 and all of our Figures) we use mn_trpkts = 0 - i.e., the whole graphs.
3.3 Viewing Graph-Image Sets
We are most interested in changes between time-bins. Therefore, in each graph-image, we show the number of traceroute packets observed on each edge. We colour the edges to show decreasing/increasing counts in shades of blue/red, and edges that were not in the previous time-bin in green. We show the nodes' enclosing outline in a different colour for the 20 ASNs with the highest number of incoming traceroute packets (in_count), and for the other nodes in black. Within each node’s outline we show its name, and below that its total in_count.
We wrote a program to create javascript viewers for each of our datasets, allowing us to explore them easily using the Firefox browser. Our viewers allow a user to move the viewing window left/right using the left/right arrow keys, as an alternative to moving the window using the browser’s scroll bars. The user may move forward/backward between time-bins using the up/down arrow keys, or by entering a time-bin number and clicking on a button at the lower left of the browser screen. When moving using the up/down keys we maintain the user’s view at the same position, thus focusing on the same section of the graph while changing time-bins. While inspecting a graph with our viewer, one may hover the browser’s cursor over any node; that causes the node’s tooltip data (ASN name and country code) to be displayed. Additionally, one can always use the browser’s ‘Find’ function (ctrl-F for Firefox) to locate a node by it’s IP address.
In the following two sets of graphs:
- We’ve used mn_trpkts = 30 so as to reduce the size of this article’s SVG images, and also the time needed to render the image for each viewed time-bin.
- We’ve chosen 5017 and 5006 as examples, because 5017 has a single instance, and 5006 has only 9, so both these msm_ids have graphs with lots of nodes at low depths.
- The label at the bottom of each screen shows the Destination ID (msm_id) the time-bin number and its corresponding time of day, e.g., 5017-20191211-0000-48-, Bin 0, 2019-12-11T00:00 UTC.
- The simplest way to view the graphs is to move the window to the bottom of the screen using its vertical scroll bar, use the horizontal scroll bar to get the destination node (drawn as a rectangle) at the bottom of the screen, then zoom in or out to adjust the number of nodes you can see on the screen. Now press the “Get Bin” button (bottom left) to get time_bin 1; after that you can use your Up/Down keys to move from bin to bin.
4. ASN Graphs
Since we are particularly interested in the AS-level Internet topology, we wrote a filter program to gather together all the nodes for each AS into a single node; on our graphs these nodes have ASNs as labels rather than IPv4 addresses. The labels at the bottom of these ASN graphs are the same as for the full graphs above.
The ASN graphs are - of course - much less cluttered than the full (node-based) graphs, making it much easier to see routing changes in the ASN-level topology.
5. Finding ‘Significant’ Changes in the Graphs
5.1 Classification Algorithm
We are interested in topology changes that last for one or more time-bins, and in two kinds of network objects: nodes and edges.
We read the graphs*.txt files for each msm_id to find all the nodes and edges for every time_bin, making node- and edge- lists, producing lists of found objects. From those lists we discard objects that were observed in all but two time_bins; we consider those to be stable, and not of interest.
For every non-stable object we make two vectors:
| presence |
1 for every time_bin in which the object was present, 0 otherwise |
|---|---|
| i_count | Number of trpkts seen for every time_bin |
From presence we compute:
| mx_orun | Longest occurrence of one or more 1s |
|---|---|
| n_oruns | Number of occurrences of one or more successive 1s |
| n_zruns, | Number of occurrences of one or more successive 0s |
We filter the lists of non_stable objects, keeping those for which:
- n.mx_orun > c.n_bins/4 In least a quarter of the day’s time-bins
and
- n.n_zruns >= 1 At least one run of zeros
and
- n.n_oruns >= n.n_zruns More one-runs than zero-runs
Filtering with this test reduces our number of objects for the two msm_ids whose graphs are linked to in section 3.4 leaves:
| msm_id | nodes | edges | |
|---|---|---|---|
| Total objects (in all bins) | 5017 | 22775 | 17431 |
| 5004 | 21950 | 16696 | |
| Non-stable objects | 5017 | 22096 | 17136 |
| 5004 | 21552 | 16526 | |
| Filtered objects | 5017 | 119 | 65 |
| 5004 | 114 | 42 |
In this table, the nodes are those that responded to at least one traceroute packet, and the edges are those between two of the responding nodes. We note that the number of edges found for each of these destinations (msm_id) is 0.76 (about three-quarters) of their number of nodes. The remaining quarter of the nodes were the most distal in our graphs, so they did not have any incoming edges.
5.2 Finding Similar Sets of Objects (nodes or edges)
We use SciPy’s linkage() function to perform clustering using the (default) Nearest Point algorithm on the filtered objects (above). To further reduce the number of objects of interest, we consider only objects that had an average of at least 72 trpkts (i.e. 3*mn_trpkts) per bin.
Using this approach, we found interesting outages for edges in msm_ids 5017 and 5004 with mn_trpkts = 24. For these two msm_ids, bar plots showing which bins those objects appeared in are as follows:
5017-24 Edge Presence bar plot
5004-24 Edge Presence bar plot
We sort those objects into groups that have the same outages (i.e., sets of 0s in their presence vectors), and print a summary of those. For example, for the edges in 5017-24 and 5004-24 we find:
5017 Edge presence: zero-runs . . .
13 edges, 281 pkts (average), zero for bin(s) <24-25>
268 for 24940->24940, 213.239.252.173->213.239.224.10
260 for 24940->24940, 213.239.252.253->213.239.224.14
263 for 24940->24940, 213.239.224.14->213.239.229.66
254 for 24940->24940, 213.239.245.222->213.239.229.66
271 for 24940->24940, 213.239.224.10->213.239.229.70
268 for 24940->24940, 213.239.245.213->213.239.229.70
263 for 24940->24940, 213.239.252.253->213.239.245.213
253 for 24940->24940, 213.239.252.173->213.239.245.222
513 for 11039|136168->24940, 195.66.227.209->213.239.252.169
234 for 7713->24940, 37.49.237.197->213.239.252.173
287 for 24940->24940, 213.239.252.169->213.239.252.173
239 for 7713->24940, 37.49.237.197->213.239.252.253
281 for 24940->24940, 213.239.252.169->213.239.252.253
1 edges, 230 pkts (average), zero for bin(s) <14-21>
230 for 1299->1299, 62.115.112.243->62.115.123.12
5004 Edge presence: zero-runs . . .
14 edges, 287 pkts (average), zero for bin(s) <5-12>
109 for 3356->3356, 4.68.127.233->4.69.143.202
112 for 11039|136168->3356, 194.149.166.50->4.69.143.202
318 for 11039|136168->3356, 194.149.166.54->4.69.143.202
146 for 5089->13335, 62.253.174.178->162.158.32.254
94 for 5607->3557, 2.127.241.243->192.5.5.241
229 for 2856->3557, 109.159.253.95->192.5.5.241
145 for 13335->3557, 162.158.32.254->192.5.5.241
1140 for 3356->3557, 195.50.116.34->192.5.5.241
418 for 11039|136168->3557, 195.66.225.179->192.5.5.241
96 for 11039|136168->3557, 195.66.244.71->192.5.5.241
125 for 5089->3557, 212.250.14.2->192.5.5.241
480 for 3356->3356, 4.68.127.233->195.50.116.34
483 for 3356->3356, 4.69.143.202->195.50.116.34
126 for 5089->5089, 62.253.175.34->212.250.14.2
2 edges, 283 pkts (average), zero for bin(s) <13, 19, 21, 29-37, 41>
289 for 7843->1280, 66.109.6.143->149.20.65.16
277 for 1280->3557, 149.20.65.16->192.5.5.2415.3 Viewing ‘Significant’ Changes in 24-trpkts Graphs
The summaries listed in section 5.2 provide sets of node pairs (edges) for objects that had the same sets of outages. We can filter our network graphs to keep only the outages appearing in such lists. To do that, we use “clip specification” files, as in the following examples, then make SVG graph-image sets for the “clipped” nodes.
We present some examples of clip specification files, followed by links to their resulting graph-image sets.
sd clip-01 # .txt in 20191211/graphs-5017-24
pbtype Edges
about Routing changes in graphs-5017-24
bins 22,23 All edges present, red/blue = decreasing/increasing
bins 25,25 No edges present
bins 26,27 All edges present again
All nodes in 213.239/16 are close to 5017’s dest, in ASN 24940
bins 22 27 # (first, last)
nodes
213.239.252.173 213.239.224.10
213.239.252.253 213.239.224.14
213.239.224.14 213.239.229.66
213.239.245.222 213.239.229.66
213.239.224.10 213.239.229.70
213.239.245.213 213.239.229.70
213.239.252.253 213.239.245.213
213.239.252.173 213.239.245.222
195.66.227.209 213.239.252.169
37.49.237.197 213.239.252.173
213.239.252.169 213.239.252.173
37.49.237.197 213.239.252.253
213.239.252.169 213.239.252.253
eofsd clip-01
pbtype Edges
about Routing changes in 20191211/graphs-5004-24
bins 3,4 All edges present
bins 5-12 No edges present
bins 13-14 All edges present again
first last, zero in <5-12>
bins 3 15 # (first, last)
nodes
4.68.127.233 194.149.166.50 194.149.166.54
4.69.143.202 62.253.175.34 62.253.174.178
162.158.32.254 212.250.14.2
94.149.166.50
94.149.166.50 4.69.143.202
4.68.127.233 4.69.143.202 195.50.116.34
2.127.241.243 109.159.253.95 162.158.32.254 # All these feed to dest
195.50.116.34 195.66.225.179 195.66.244.71 212.250.14.2
192.5.5.241 # Dest
eof5.4 Viewing ‘Significant’ Changes in 24-trpkts ASN Graphs
Of course the approach presented in section 5.2 above also works for ASN graphs! For example, in the Edges summaries for 5017-asn-24 and 5004-asn-24 we find:
5017 ASN Edge presence: zero-runs . . .
1 edges, 121 pkts (average), zero for bin(s) <8>
121 for 5410->7713
1 edges, 133 pkts (average), zero for bin(s) <39-41>
133 for 5511->1299
sd clip-01
pbtype Edges
about Routing changes in 20191211/graphs-5017-asn-24
ASNs 5410 and 7713 route disappears for bin 8
bins 6 10 # bn_lo (first), bn_hi (last)
nodes
5410 7713
# 24940 # Dest
eofsd clip-02
pbtype Edges
about Routing changes in 20191211/graphs-5017-asn-24
ASNs 5511 and 1299 route disappears bins 39-41
but routes around them are much more stable
bins 37 43 # bn_lo (first), bn_hi (last)
nodes
11039|136168
5511
6453 1299
24940 # Dest
eof5004 ASN Edge presence: zero-runs . . .
5 edges, 260 pkts (average), zero for bin(s) <5-12>
112 for 786->11039|136168
292 for 5089->13335
458 for 2856->3557
250 for 5089->3557
189 for 5607->3557
1 edges, 219 pkts (average), zero for bin(s) <39-44>
219 for 7527->3557
2 edges, 568 pkts (average), zero for bin(s) <13, 19, 21, 29-37, 41>
578 for 7843->1280
558 for 1280->3557
sd clip-01
pbtype Edges
about Routing changes in 20191211/graphs-5004-asn-24
ASNs 5511 and 1299 route disappears bins 39-41,
but routes around them are much more stable
bins 37 43 # bn_lo (first, last)
nodes
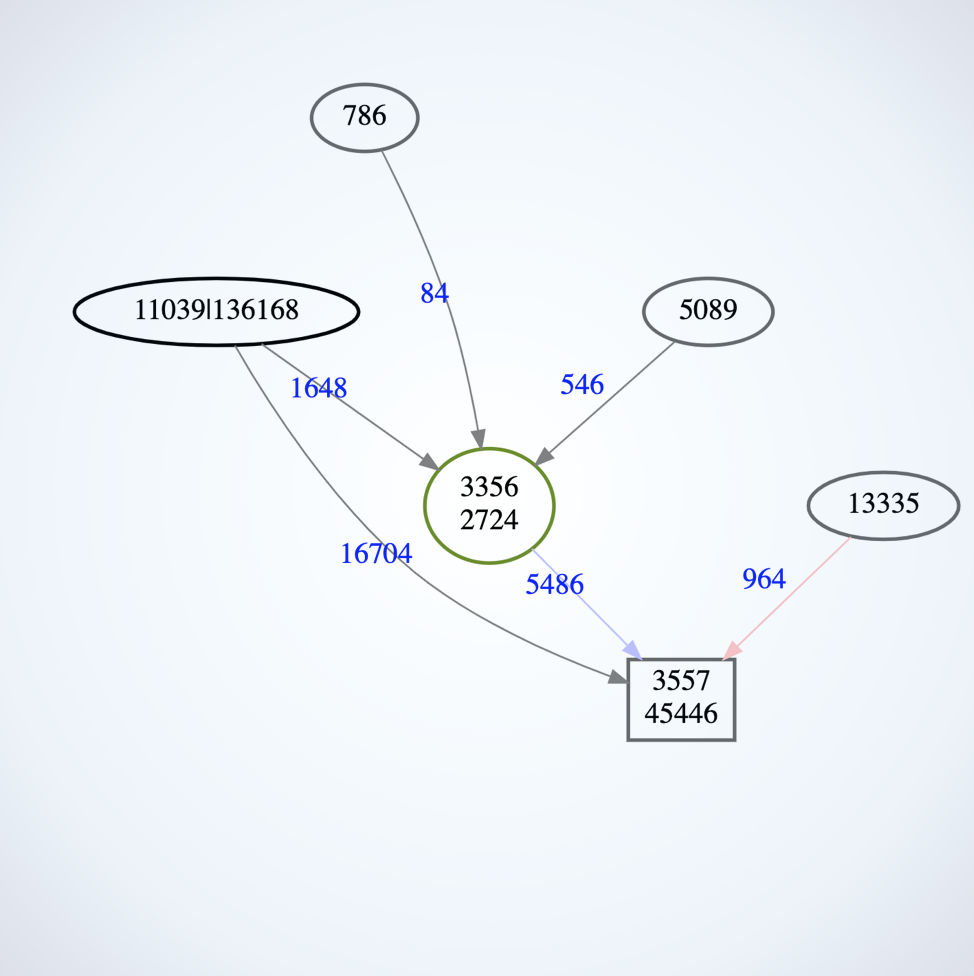
786 11039|136168
5089 13335
2856 5089
3356
3557 # Dest
eofsd clip-02
pbtype Edges
about Routing changes in 20191211/graphs-5004-asn-24
bin 37 ASN 7527 connected, 222 trpkts
bin 38 ASN 7527 connected, 78 trpkts
bins 39-44 ASN 7527 disconnected
bin 45 ASN 7527 connected, 174 trpkts
bin 46 ASN 7527 connected, 222 trpkts
bins 37 46 # (first, last)
nodes
7527
3557 # Dest
eofsd clip-03
pbtype Edges
about Routing changes in 20191211/graphs-5004-asn-24
ASNs 7843 and 1280 are mostly stable with about 662 trpkts
They are disconnected for bins 13, 19, 21, 29-37 and 41,
and stable with about 640 trpkts after that
bins 11 43 # bn_lo (first, last)
nodes
7843 1280
3557 # Dest
eofNote: In our ASN graphs, the disappearance of a node (ASN) means that traceroute packets from RIPE Atlas probes did not reach that ASN. As a result, all nodes within that ASN lost Internet connectivity!
6. Conclusion
6.1 Overview
Considering our list of questions posed in section 1:
Q1. How do we choose the ‘best’ RIPE Atlas traceroute Destination?
Section 2 covers the collection of our data. We computed statistics for all the time_bins in each of our six chosen measurement IDs (msm_ids), and explored their statistics (Figures 1 to 6). From our six datasets, 5017 and 5006 have small numbers of destination instances (1 and 6), so they give rise to graphs with easily viewable nodes at low depths. As well, we used 5017 and 5004 in section 5 because we were able to make outage summaries for them that showed large numbers of traceroute packets being lost for 1- to 6-hour periods.
Q2. How can we visualise the Topology from our topology graphs?
Section 3 presents our methods for drawing graphs of nodes for each time-bin in our 2019 datasets, producing graph sets of SVG images, and making javascript viewers for each graph set.
Section 4 describes our method of filtering node graphs so as to create ASN graphs. It demonstrates that our graph creation and viewing methods work well for the ASN graphs, and are useful for finding ASN outages.
Q3. How can we find ‘significant’ topology changes in our graphs?
Section 5.1 presents our algorithm for finding such topology changes, and using it to filter our graphs to make sets of non-stable nodes and edges. In section 5.2 we use Nearest Point clustering to find sets of nodes or edges that had outages in the same time-bins, and are able to draw bar plots for nodes or edges that clearly show the resulting clusters.
Q4. Can we find a way to visualise those changes?
In section 5.3 we created a simple method of using our summary information to make “clips”, i.e., subsets of an msm_id’s graphs. These make it much easier to see what changes occurred - doing that by inspecting the full graphs is extremely difficult!
Overall, we now have useful tools for finding and viewing “significant” outages in the global Internet.
6.2 Future Work
- Repeat this work for IPv6 network nodes, and compare IPv6 connectivity to that of IPv4.
- Collect RIPE Atlas data using a continuous stream, and process it at regular intervals, for example, hourly. Such a system could raise alerts whenever significant outages occur.
- Design a “weaponised” version suitable for alerting ISPs when outages are recognised.
6.3 Reproducibility
All the Python programs developed during this project are publicly available on github.

Comments 0
The comments section is closed for articles published more than a year ago. If you'd like to inform us of any issues, please contact us.